Besides an investment manager simply making more money than a passive strategy, there is another issue: Although the strategy of investing in every stock appeared to perform better than 75 percent of investment managers, the price of the stock market as a whole fluctuates up and down, and could be on a downward decline for many years before returning to its previous price.
The passive strategy appeared to generate the market-beating return over periods of 10 years or more. This strategy may be risky for those who feel they might need to withdraw their money before a 10-year holding period, for example. Thus investment managers who employ a strategy which is less likely to lose money in a particular year are often chosen by those investors who feel that they might need to withdraw their money sooner.
The measure of the correlated volatility of an investment (or an investment manager's track record) relative to the entire market is called beta. Note the "correlated" modifier: an investment can be twice as volatile as the total market, but if its correlation with the market is only 0.5, its beta to the market will be 1.
Investors can use both alpha and beta to judge a manager's performance. If the manager has had a high alpha, but also a high beta, investors might not find that acceptable, because of the chance they might have to withdraw their money when the investment is doing poorly.
These concepts not only apply to investment managers, but to any kind of investment.

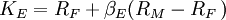
![\beta_E = \beta =\left[ \beta_A - \beta_D \left(\frac {D}{V}\right) \right] \frac {V}{E}](http://upload.wikimedia.org/math/8/8/6/886efee7ec7edade19175a572534f9a7.png)


 ,
,
