By definition, the market itself has an underlying beta of 1.0, and individual stocks are ranked according to how much they deviate from the macro market (for simplicity purposes, the S&P 500 is usually used as a proxy for the market as a whole). A stock that swings more than the market (i.e. more volatile) over time has a beta whose absolute value is above 1.0. If a stock moves less than the market, the absolute value of the stock's beta is less than 1.0.
More specifically, a stock that has a beta of 2 follows the market in an overall decline or growth, but does so by a factor of 2; meaning when the market has an overall decline of 3% a stock with a beta of 2 will fall 6%. Betas can also be negative, meaning the stock moves in the opposite direction of the market: a stock with a beta of -3 would decline 9% when the market goes up 3% and conversely would climb 9% if the market fell by 3%.
Higher-beta stocks mean greater volatility and are therefore considered to be riskier, but are in turn supposed to provide a potential for higher returns; low-beta stocks pose less risk but also lower returns. In the same way a stock's beta shows its relation to market shifts, it also is used as an indicator for required returns on investment (ROI). If the market with a beta of 1 has an expected return increase of 8%, a stock with a beta of 1.5 should increase return by 12%.
This expected return on equity, or equivalently, a firm's cost of equity, can be estimated using the Capital Asset Pricing Model (CAPM). According to the model, the expected return on equity is a function of a firm's equity beta (βE) which, in turn, is a function of both leverage and asset risk (βA):
where:
- KE = firm's cost of equity
- RF = risk-free rate (the rate of return on a "risk free investment", e.g. U.S. Treasury Bonds)
- RM = return on the market portfolio
![\beta_E = \beta =\left[ \beta_A - \beta_D \left(\frac {D}{V}\right) \right] \frac {V}{E}](http://upload.wikimedia.org/math/8/8/6/886efee7ec7edade19175a572534f9a7.png)
because:
and
- Firm Value (V) = Debt Value (D) + Equity Value (E)

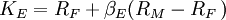


No comments:
Post a Comment